Abaqus自适应网格之一：ALE adaptive meshing（上）

ALE adaptive meshing (Arbitrary Lagrangian-Eulerian analysis) 在分析过程中对网格进行实时动态调整，可以在整个分析过程中保持高质量网格。具有如下特点：

1 允许网格独立于材料移动，即使在发生大变形或材质缺失时也可保证网格质量。不改变网格拓扑关系，若要在极端变形时保持高质量网格则会存在一些限制。

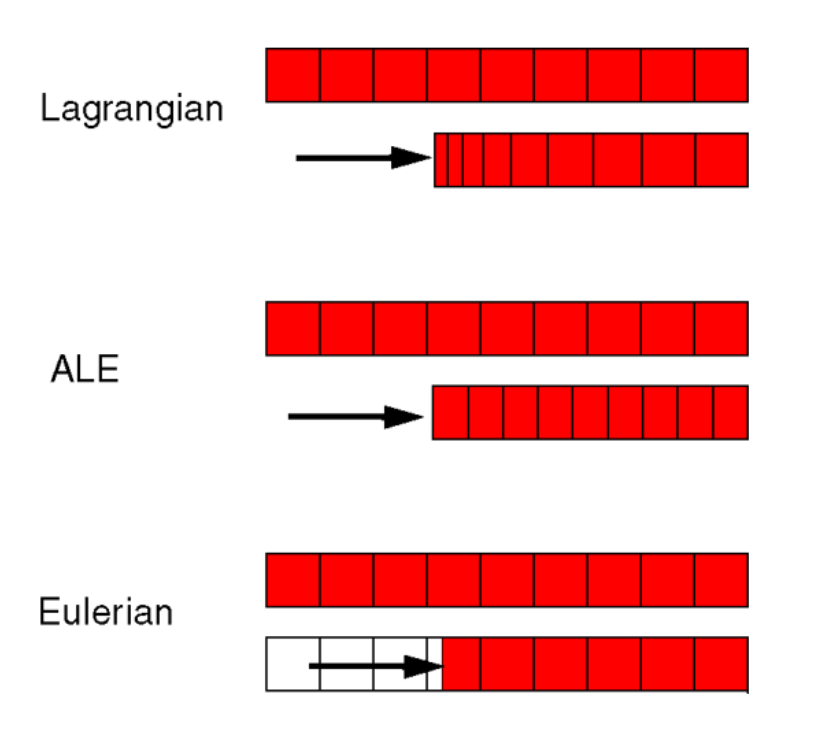
2 与Lagrangian analysis和Eulerian analysis之间的异同，如图1所示：

1) Lagrangian analysis:节点固定在材料内，单元随着材料变形而变形。单元由单个材料100%充满，材料边界与单元边界重合；

2) Eulerian analysis:节点在空间中固定，在材料流过时单元不变形。支持单个单元包含多种材料和孔隙，因此，必须在每个时间增量期间计算边界条件，材料边界和单元边界无必然联系；

3) ALE adaptive meshing:单个单元必须由一种材料100%充满。模型中材料的受限于单元的变形，故而可以精确定义材料边界和复杂的接触相互作用。

3 Abaqus/Explicit中的ALE mesh旨在模拟大变形问题。不会最小化小变形分析中的离散化误差。在Abaqus/Standard中则主要用于声学领域和模拟材料的烧蚀或磨损效应。

1 ALE adaptive Mesh Domain

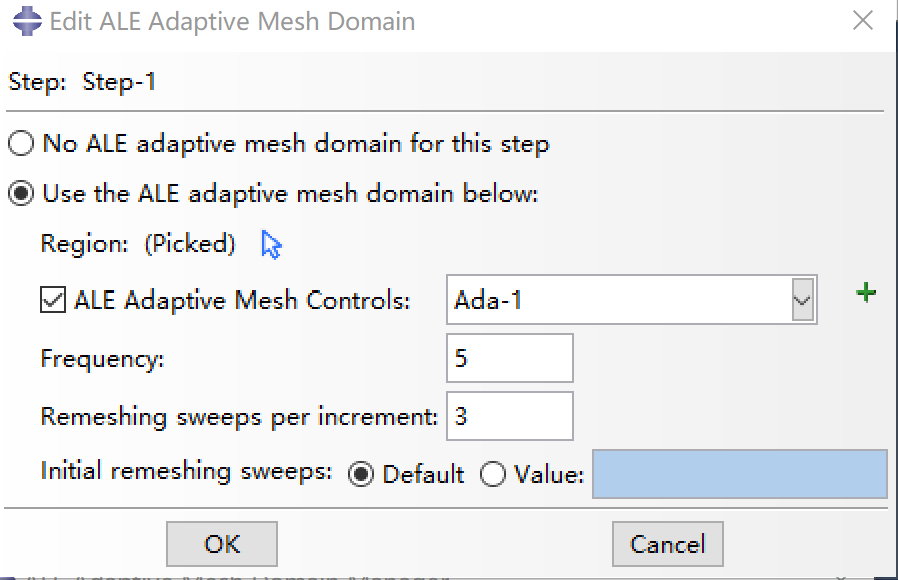
自适应网格区域有Lagrangian和Eulerian两种。前者(transient dynamics large deformation)，网格沿着垂直于边界的方向移动，后者(steady-static, material flow)，在一些自定义边界条件中，材料可以流入或流出网格，默认条件下，区域边界上的网格不固定，必须在Mesh Constraint中设置约束。

1.1 Frequency

通常情况下，频率是影响网格质量和效率的主要参数。前者(transient dynamics large deformation)，每5-100个增量步，需要对网格重构一次；后者(steady-static, material flow)需要的频率则更高。默认情况下，前者取1后者取10。

1.2 Remeshing sweep per increments

在每个自适应网格增量过程中，通过一个或多个扫掠生成新网格，然后将参量在网格中平流化，以此获得新网格。

在自适应网格增量中，对自适应网格域进行迭代扫掠来创建一个更平滑的网格。随着扫掠次数的增加，自适应网格划分的强度也相应增加。默认为1。

1.3 Initial remeshing sweeps

当执行初始网格扫描时，初始条件被平流到新网格。如果初始网格包含高度扭曲单元时，在计算开始之前对网格进行平滑处理，以便在整个步骤中使用高质量网格。对于uniform smoothing objective，默认执行5次网格扫掠。对于graded smoothing objective，默认执行两次网格扫掠，不考虑渐变。在所有后续的网格扫描中用于分级的长宽比基于该局部平滑网格。

相关文章

ABAQUS价格
ABAQUS软件介绍